Dynamic formations

CrowdMaster has the ability to dynamically assign agents to points in a formation in a natural looking manner without the user assigning agents to positions explicitly. This might be useful in situations where agents need to converge and create a formation but where the user can’t guarantee the order of arrival at the formation location.

At the heart of CrowdMasters dynamic formation system is a divide and conquer point cloud pairing algorithm inspired by quick sort and optical flow algorithms. The aim is to match every point in an input point cloud to a point in a target point cloud in a natural way. By natural I mean we want to avoid the situation where most agents are assigned nearby target points but a small number are assigned far away points. This might be the case if using an optimisation algorithm.

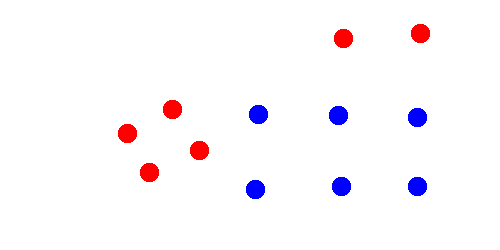
For example, the red dots represent input points and the blue dots represent points in the target formation.

The method works using the following steps:

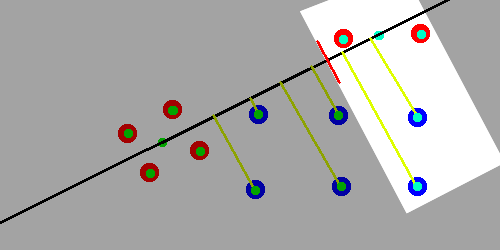
1) Select two points from the input point cloud and use these as the start points for the k-mean method. Do a small number of iterations of the k-mean algorithm to form two spacially separated groups A and B. ( O(n) )

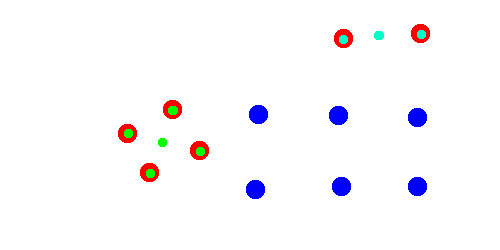
The green and turquoise dots represent the two groups and their centres.

2) Project each point in the target point cloud onto the line between the mean positions of all points in A and in B. Split the target points into two groups with size equal to A and B (called A’ and B’) where the points in A’ are points that were projected to the line on the same side of the divide as the mean position of A. ( O(n) using quick select. O(n log n) using quick sort )

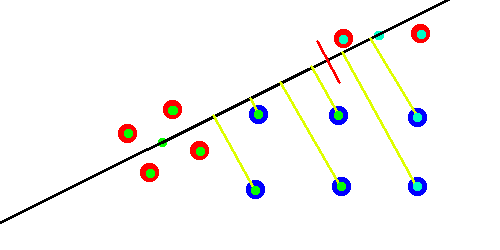
The black line is the line between the centres of the groups and the yellow lines are showing where each target point is projected along that line.

3) Repeat the process for A & A’ and separately for B & B’ (recursive call)

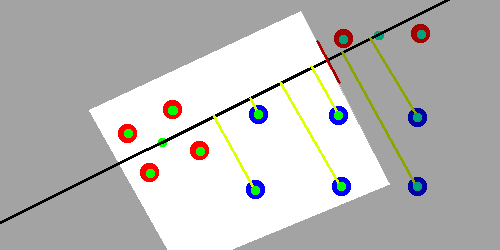
Larger groups may recurse and repeat the process.

4) If there are less than C (where C is a small constant) agents in A or B then calculate all pairings and select the optimal. ( O(1) )

Small groups will brute force a solution.

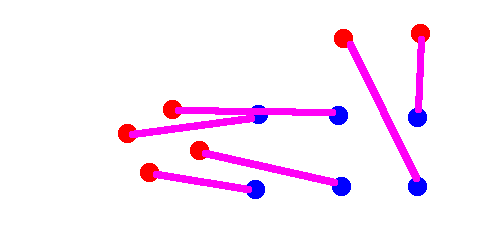
The resulting pairs for this example might look something like this.

Advantages:

• O(n log n) run time.
• Produces natural looking results
• Trivial to handle cases with different sizes of input and target point clouds.
• If agents move directly from their start position to end position at a constant rate there should be very little overlap. This means that even with some extra steering behaviour the need for good collision avoidance between agents is reduced.

Disadvantages:

• Small changes to input can lead to very different outputs.
• Python provides fast sort function which for the desired number of agents works faster than a custom Python quick select function however make the asymptotic runtime O(n^2). However, in practice this method still runs very quickly for all reasonable inputs.